Linear Regression
LR.
Linear Regression is an important introductary topic for those who are starting out in machine learning / statistics.
Understanding the main concept behind it is essential as it will allow you to transition into other complex algorithms.
Linear Regression falls under Supervised Learning. This means we are provided with the input and output values, and we try to predict an outcome based on this information. As the name suggests, Linear regression is a form of regression analysis (as opposed to Classification). In this instance, we are trying to predict a continious variable i.e temperature or prices instead of labels.
The Aim
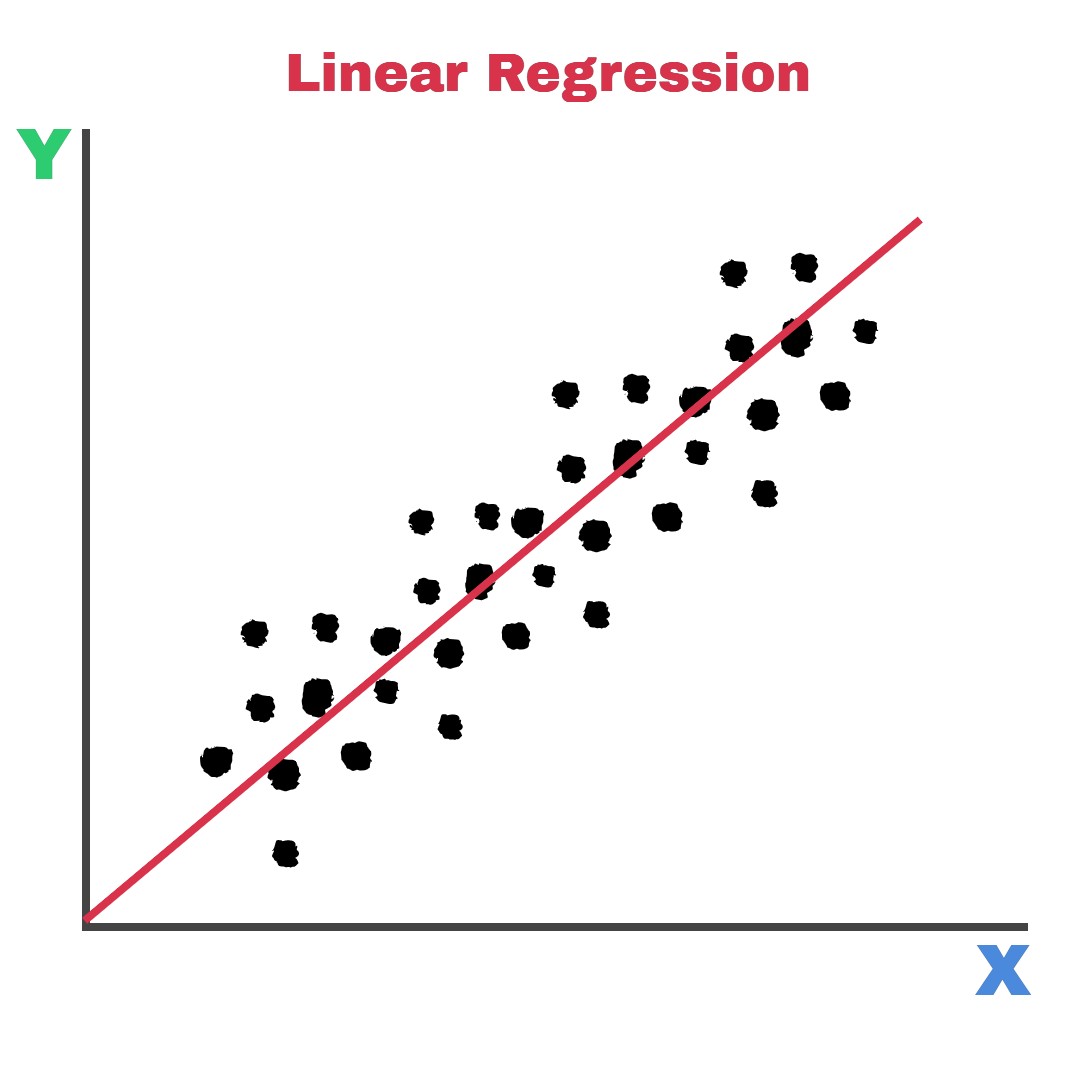
The aim of linear regression is simple: we want to draw a line which fits our data the best!. The line of best fit is the line which which is obtained after minimizing the error. Usually, it is the sum of squared error (SSE).
Straight Line Equation
But before we get into detail on minimizing the SSE, we must first know the equation used to draw a straight line. This equation, which you most likely have come accross at somepoint is \(y = mx + b\). (Note that it can be expressed in other forms such as y=ax+b etc..). Lets break it down:
- y represents the dependent variable (the variable that we measured)
- m is the slope (the gradient of the line)
- x is the indepent variable (the variable we change)
- b is the y-intercept
assumptions
It is important to know that the main assumption of Linear Regression, as the name suggests, is that the relationship between X and Y is linear. If the data is linear, we can assume that our predictions will be accurate.